Oyun teorisi ile ilgili olarak daha önce de hem burada hem de eski blog’umda yazmıştım. NE (Nash Equilibrium)’un oyun teorisinin ne kadar köklü bir noktası olduğundan da bahsetmiştim. Şimdi karar verme ve durumlar karşısındaki duruşumuzu belirleme aşamasında bize nasıl yardımcı olabileceği başlığını biraz açmak istiyorum.
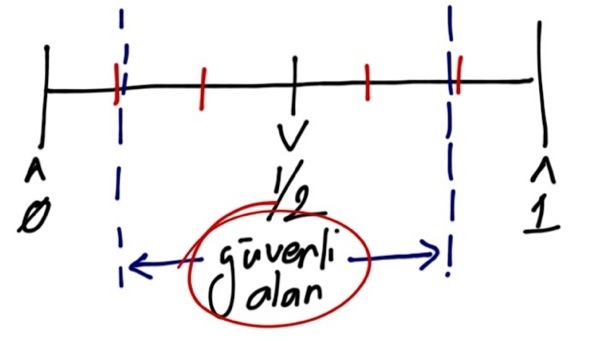
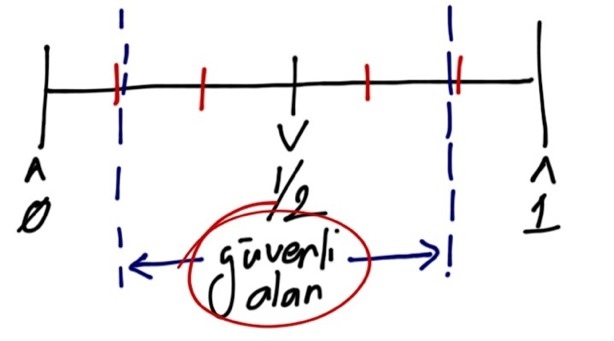
Yukarıdaki resimde gördüğünüz skalayı 2 boyutlu bir oyun gibi düşünün.
Örneğin sağ ve sol partiler. 0 sağ, 1 ise sol olsun. Bu aralıkta da 100 kişi eşit aralıklarla dağılmış olsun. Yani 0’da aşırı sağcı ve 1’de tersi. Her seçmen oy kullanmak zorunda ve, her biri de kendine en yakın hissettiği adaya oy versin. Her seçmen de isterse aday olabilsin.
Bu durumda oyun kurgumuzu tamamlamış oluyoruz (kazanç seçimi kazanmak tabii ki).
Her durumda seçmenlerin aday olup olmama hakkı saklı olduğuna göre ideal durumda 1/2’deki (yani tam ortadaki, 50.) seçmenin aday olduğu senaryo bir NE’dir. Ancak bu düzlemde NE sadece 1 adet değil. Örneğin; 1/3 ve 2/3’deki seçmenler aday olursa ortada ki aday seçimi kaybedecektir. Bu diğer seçmenlerin aday olma durumlarının NE’yi nasıl değiştirdiğine çok güzel bir örnek.
Bu 0-1 skalasındaki oyun’da kazanma şansları diğer adaylara göre daha düşük olan ve dolayısı ile ASLA NE OLMAYACAK seçmenler 1/6-5/6 skalası dışında kalan adaylardır. 1/6’daki seçmenin aday olması durumda, ideal senaryodaki (1/2’deki) seçmenin aday olması hala NE’dir.
Neyse; konumuz aslında oyun teorisini anlatmak değil. Median seçmenler (ve adaylar) eşit bir dağılımda her zaman için daha şanslılar. Bu zaten aşikar. Ancak bu örnek bize uçların ne kadar kendilerini şanssızlaştırdıklarını gösteriyor. Median olmaktan ne kadar uzaklaşırsanız, o kadar seçilme şansınızı azaltırsınız kısacası. Gerçek dünya tabii ki ders kitaplarından 1:1 uygulama ile çözümlenemez, ancak kalnınızı kurarken nerede durduğunuzu ve durmamanız gerektiğini unutmamak önemli.